ISO 14971 Fundamentals: A primer on P1, P2 and how they relate to probability of harm

There is a lot of confusion in the device industry about basic probability concepts, which often leads to incorrect application in practice. Here is a primer to help build a deeper understanding.

The relationship between P1, P2 and the probability of occurrence of harm (P) is quite simple and straightforward, as illustrated in Figure C.1 in Annex C of the current 3rd edition of ISO 14971¹:

P = P1 * P2

As a reminder,

P1 = Probability of a hazardous situation occurring; and

P2 = Probability of a hazardous situation leading to harm.

Yet, there is still a lot of confusion about this fundamental relationship, and risk practitioner continue to be challenged in applying it correctly when estimating risk(s) associated with their medical device.

In a recent LinkedIn poll², more than half of the respondents got this question wrong:

Figure 1: LinkedIn poll results, September 2024.

The correct answer is 1 in 5000.

In this scenario, we are given the information that an individual risk of harm is considered to be acceptable at a rate of 1 in 10,000. The S=5 (Severity level 5) is irrelevant information. We are also given the information that P2 has been estimated to be 0.5.

Applying the formula P (of harm) = P1 * P2; we can easily estimate the maximum tolerable P1 by dividing 1/10000 by 0.5.

---

Lack of understanding leads to confusion and inconsistency in industry practice

These poll results reflect a general lack of understanding of basic probability concepts. As a result, industry practice has evolved to assigning numerical ranks to P1 and P2 on a 1-5 scale based on qualitative or semi-quantitative attributes. Often, these tables are modeled after the examples of tables in ISO/TR 24971³.

Next, these P1 and P2 ranks are combined in an arbitrary P1 x P2 table to yield another 1-5 scale for assigning a rank to the overall probability of occurrence of harm (P).

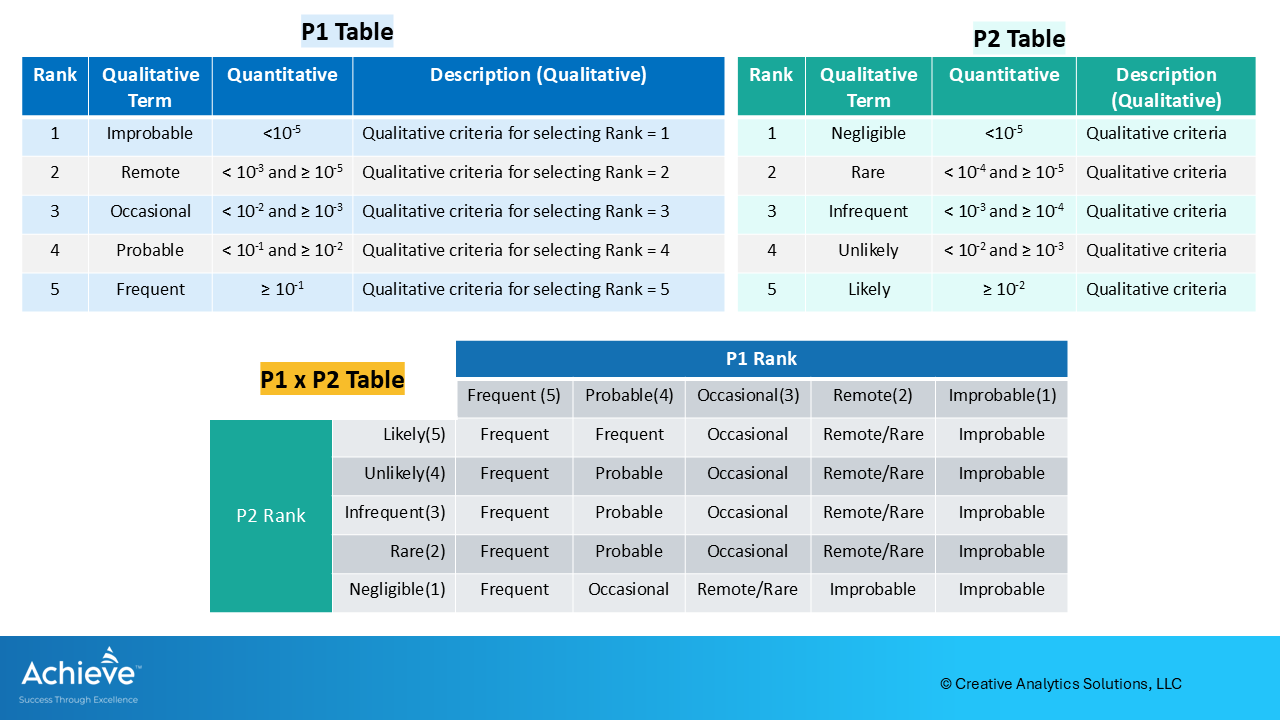
As an example, it is not uncommon to come across P1, P2 and P1xP2 combination tables shown below⁴:

Figure 2: Illustrative examples of P1, P2 and Combined P1xP2 tables

Note that there is no mathematical basis for the various combinations of P1 and P2 in the combined P1 x P2 table illustrated in Figure 2 above. As a result, there is a high likelihood of inconsistent application leading to inaccuracies in risk estimation.

Let us consider the following example to understand how this approach can lead to inconsistencies :

• Let us consider a scenario where P1 is assigned a rank of 3 (Occasional) based on some qualitative criteria. A P2 rank of 5 (Likely) is assigned based on another set of qualitative criteria.

• Using the P1xP2 table in Figure 2, we find that the combined rank for P1 = 3 (Occasional) and P2 = 5 (Likely) is also Occasional (intersection of 3rd column and 1st row in the P1xP2 table above).

• Now let us consider another scenario where P1 is assigned a rank of 5 (Frequent) and P2 is assigned a rank of 3 (Infrequent).

• Using the P1xP2 table in Figure 2 again, we find that the combined rank for P1 x P2 in this case is Frequent (intersection of 1st column and 3rd row in the P1xP2 table above).

As a result, we would estimate the probability of harm as Occasional (rank = 3) in the first scenario, and Frequent (rank = 5) in the second scenario above. The same combination of the two ranks, in different order, results in two different ranks for the overall probability.

Notice that when P1=1 (Improbable), the combined P1xP2 is always Improbable (rank=1) regardless of the P2 rank. On the other extreme, when P1=5(Frequent), the combined P1xP2 is always Frequent (rank=5) regardless of the P2 rank.

It seems that the combined P1xP2 table is biased toward the P1 rank!

This is just one example of the inconsistency that can result from using arbitrarily created qualitative or semi-quantitative tables instead of using a mathematical approach based on principles of probability.

This article offers a quick review of the fundamental concepts in probability to help build a better understanding for practical applications.

---

Let us review 2 fundamental principles

According to ISO 14971, the following two principles apply to the hazard-harm relationship:

1. Exposure to hazard(s) is required for a hazardous situation to occur; and

2. Harm cannot occur if there is no exposure.

These principles are illustrated in the figure below:

Figure 3: Hazard-harm relationship. Source: ACHIEVE Training.

Let us apply basic probability to understand P1, P2 and relationship to the overall probability of harm

A basic concept in probability is that the probability of occurrence of an event (say A) is given by the following equation

P(A) = X/T; where

X = Number of ways event A occurs; and

T = Total number of elementary outcomes

Unless we have a basic knowledge of the process, probability is estimated using a sample of observations. This is also known as empirical probability, which is different from the a priori probability, where we have a fundamental understanding of the process, for example, a coin toss or drawing a card from a standard deck.

Let us now consider our specific situation related to the probability of occurrence of harm (P) and how it is related to P1, and P2. One way to visualize this situation, and associated probabilities is by using a decision-tree like diagram as shown in Figure 4 below:

Figure 4: Relationship between hazard, hazardous situation and harm, and associated probabilities.

In Figure 4 above:

• Event type A = Hazardous situation occurs; Event type A' = Hazardous situation does not occur

• Event type B = Harm occurs; Event type B' = Harm does not occur

• P(A) = Probability of occurrence of a hazardous situation (P1 in ISO 14971 terminology)

• P(A') = Probability that a hazardous situation does not occur

• P(B) = Probability of occurrence of harm (P in ISO 14971 terminology)

• P(B') = Probability that harm does not occur

• P(B|A) = Probability that harm occurs when a hazardous situation has occurred (P2 in ISO 14971 terminology)

• P(B'|A) = Probability that harm does not occur when a hazardous situation has occurred

• P(B'|A') = Probability that harm does not occur when a hazardous situation has not occurred (by definition, this should be equal to 1).

• P(B|A') = Probability that harm occurs when a hazardous situation has not occurred. By definition, this is equal to 0; therefore it is not shown in the illustration above.

Consider the following example for calculating simple probabilities

Let us say we have good quality data for a medical device from the field where it was used in 1000 surgical procedures:

Figure 5: Contingency table of data from a sample of 1000 surgical procedures using a medical device.

Using the data in Figure 5, we can easily estimate some of the simple probabilities illustrated in Figure 4.

• P(A) = Total count of hazardous situations/Total procedures = 100/1000 = 0.1 (This is also the same as P1).

• P(A') = Total count of no hazardous situations/Total procedures = 900/1000 = 0.9 (this is also equal to 1-P(A), because there are only two outcomes for A and their total probability should add to 1).

• P(B) = Total count of harms/Total procedures = 10/1000 = 0.01.

• P(B') = Total count of no harms/Total procedures = 990/1000 = 0.99. (Again, this is also equal to 1-P(B), because there are only two outcomes for B and their total probability should add to 1).

Here is how we can estimate P(B|A), or P2

This is also called a conditional probability, because the probability of event B (i.e. a harm), in this case, is contingent on the probability of event A (i.e. a hazardous situation). We know this to be a key principle of hazard/harm relationship as noted above.

Notice the following data points in Figure 5:

• There are only 10 cases where a harm has occurred when a hazardous situation occurred (top row, first cell -> Hazardous situation occurs = Yes, Harm occurs = Yes).

• There are a total of 100 occurrences of hazardous situations (Top row, last cell).

Therefore, we can use the basic probability equation to estimate this conditional probability:

P(B|A) = 10/100 = 0.1

Note that it is only by a coincidence that P(A), i.e. P1, and P(B|A), i.e. P2 are both equal to 0.1. This is an artifact of the data and not because of any fundamental relationship between the two.

Notice an interesting scenario above:

• The numerator in the P(B|A) equation above is equal to 10; exactly the number of cases where a harm occurred.

• The denominator in the P(B|A) equation is equal to 100; exactly the total number of hazardous situations.

Therefore, we can also use the following equation for P(B|A):

P(B|A) = Total count of harm events/Total count of hazardous situations

=> P(B|A) =P(A and B)/P(A) = (10/1000)/(100/1000) = 0.1

We can now establish a mathematical relationship between P, P1 and P2

• Notice that by definition, P(A and B), also called the joint probability is equal to (B), the probability of occurrence of harm in our case. This is because there is only one way a harm can occur; when a hazardous situation has occurred.

• Therefore, we can re-write the P(B|A) equation above as:

=> P(B|A) = P(B)/P(A); or P2=P/P1

• Rearranging this equation, we arrive at the mathematical equation in ISO 14971:

=> P(B) = P(B|A) x P(A); or P = P2 x P1; or P = P1 x P2.

Understanding P1, P2 in the context of Bayes’ Theorem

You may have come across the following equation in the context of P(B|A):

=> P(B|A) = P(A|B) * P(B) /P(A)

This is also known as the Bayes' theorem, which is essentially a rule that can be used to revise the probability estimates of an "effect" given some prior information about relevant factors, or "causes". As an example, if we know that a patient's age (or a comorbidity) is a factor affecting the probability of occurrence of harm, we can revise our estimated probability with this a priori knowledge.

We don't need to use the Bayes' theorem to develop the P = P1xP2 relationship as a general rule.

However, the equation above still works. Let us take a closer look:

• Remember, event type A in our analysis is a hazardous situation, and event type B is a harm.

• Therefore we can understand P(A|B) as a conditional probability of occurrence of a hazardous situation given that a harm has occurred.

• We know, from the fundamental concept, that a harm cannot occur if there is no hazardous situation. This means that if a harm has occurred, then a hazardous situation must also have occurred.

• Therefore, in our analysis, P(A|B) = 1.

• We can understand this result using the data in Figure 3. There are only 10 counts of harm, and all 10 correspond to an occurrence of a hazardous situation (top row, first cell).

• If we substitute P(A|B) = 1 in the Bayes' rule above, we get to the following equation

=> P(B|A) = 1 * P(B)/P(A)

• Rearranging this equation, we again arrive at the mathematical equation in ISO 14971:

=> P(B) = P(B|A) x P(A); or P = P2 x P1; or P = P1 x P2.

Therefore, there is no need to be confused about the application of the Bayes' rule as it relates to the fundamental relationship between P, P1 and P2.

In a future article, we will review a few applications of the Bayes' rule to illustrate how the probability of occurrence of harm can be revised based on a priori information such as patient's age, comorbidities etc.

In conclusion

The relationship between P1, P2 and the overall probability of occurrence of harm, P, is simple and mathematically consistent with basic probability theory. Yet, there continues to be a general lack of understanding of these basic concepts in the medical device industry. As a result, current industry practice often leads to confusion and inconsistency in risk estimation.

It is important to note that occurrence of harm is contingent upon the occurrence of a hazardous situation. Further, there is a conditional probability, P2, that is associated with the occurrence of harm once a hazardous situation has occurred. By understanding these foundational principles, we can easily apply the P=P1xP2 equation with full mathematical rigor without having to rely on arbitrarily created qualitative or semi-quantitative probability tables.

1. ISO 14971: Medical devices - Application of risk management to medical devices, 3rd edition, issued 2019.

2. See the LinkedIn poll and discussion here.

3. ISO/TR 24971:2020 - Medical devices - Guidance on the application of ISO 14971. See tables 3 and 5, and Figure 4 in Clause 5.5 on Risk Estimation.

4. Note: For illustration purposes only. These examples do not reflect actual tables being used at any individual medical device company.